El tubo de Pitot

por Oscar E. Piro

Salto a la notoriedad

En la madrugada del 1º de Junio de 2009, el vuelo Air France 447 Río de Janeiro-París realizado con un avión Airbus 330 que llevaba 228 personas a bordo, se encontraba atravesando una violenta tormenta tropical cuando se precipitó al Océano Atlántico a unas 650 Kms al norte de las Islas de Fernando de Noronha, ubicadas a unos 400 Kms al este de la proyección más oriental del norte de Brasil. Debido a la falta de información detallada sobre el accidente, particularmente las dificultades en recuperar la llamada “caja negra” del avión, que se hundió a la profundidad de 4000 m del mar en esa región, aún no hay consenso sobre las causas del accidente. Sin embargo, una de las sospechas más firmes es que la inconsistencia entre las medidas de velocidad del aire provista por los tres tubos de Pitot que portaba la aeronave fue el origen en una cadena de eventos que concluyó con la caída ‘a pique’ del avión en el mar.

El malfuncionamiento de tubos de Pitot ha sido también la causa atribuida a otros accidentes aéreos y es particularmente clara su responsabilidad en el caso del vuelo Austral 2553 realizado por un avión Douglas DC-9 que se precipitó a tierra en Fray Bentos, Uruguay, el 10 de octubre de 1997. Como resultado de este accidente fallecieron las 74 personas a bordo del avión. La aeronave, que iba de Posadas a Buenos Aires, debió desviar su recorrido a través de Fray Bentos para evitar una tormenta. De acuerdo a la des-grabación de la “caja negra”, el indicador de velocidad comenzó a bajar a un valor que resultaba peligroso a esa altura, por lo que los pilotos aumentaron la potencia de las turbinas. Dado que la lectura de velocidad seguía bajando, el piloto decidió (tal como lo habían entrenado) posicionar los “slats” (superficies flexibles del borde delantero del ala) para no perder sustentación. Sin embargo, al hacerlo uno de ellos se desprendió casi instantáneamente, causando una asimetría en las alas y así provocando que el avión hiciera un trompo y cayera en picada en cuestión de segundos. De acuerdo a la investigación realizada, el tubo de Pitot se habría congelado al atravesar una nube (a las alturas de vuelo, la temperatura de la atmósfera puede decender hasta unos 50ºC bajo cero) y no funcionaron ni los mecanismos de descongelamiento ni la alarma que previene de la situación. El desprendimiento del slat, cuyo posicionamiento era indicado por una medida subvaluada de la velocidad del aire indicada por el Pitot, se debió a que, en realidad, los pilotos engañados por la indicación falsa de los instrumentos habían subido la potencia hasta llegar a los 1100 km por hora (kph), muy por arriba de la velocidad de crucero de este tipo de avión. En plena caída, la caja negra registró un aumento de velocidad de 300 a 800 kph en tres segundos, lo cual sólo puede indicar un repentino descongelamiento del tubo de Pitot. Se estima que el avión cayó 'en picada' a una velocidad de 1200 kph, dejando un cráter de unos 70 metros de largo y 10 de profundidad.

Porqué la medida de la velocidad del aire es tan importante en aeronavegación? Los aviones modernos vuelan en condiciones operativas estrictas, y es peligroso volar a velocidades demasiado bajas (respecto del aire), porque la aeronave puede entrar en pérdida de sustentación (“stall”) y también a velocidades excesivas por razones estructurales. Así es que los controles manuales y automáticos del avión deben monitorear constantemente la velocidad de la aeronave respecto del aire circundante. Curiosamente, estas medidas se realizan con un instrumento inventado a inicios del siglo XVIII por el físico e ingeniero hidráulico francés Henri Pitot para medir la velocidad de la corriente en ríos y canales y de embarcaciones. En su aplicación a la aeronavegación, su funcionamiento se basa en la medida de la velocidad del aire mediante un principio físico sorprendentemente simple, similar a monitorear la velocidad de un automóvil sacando la mano por la ventanilla del vehículo y experimentar la tensión muscular necesaria para mantenerla en la corriente de aire.

Fundamentos hidráulicos del tubo de Pitot

Líquido en reposo

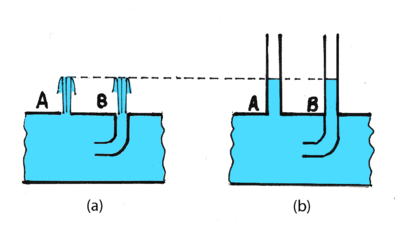
Si en un conducto conteniendo agua a presión en reposo practicamos un par de agujeros A y B, con la abertura B conectada a un tubo curvado a 90º como indica la Figura 1a, notaremos la formación de sendas surgentes que alcanzan la misma altura (no importa la forma de las aberturas: Principio de Pascal), tanto más grande cuanto mayor es la presión del agua. Si insertamos sendos tubos verticales en las aberturas A y B como muestra la Figura 1b, el agua se acumula en dichos tubos hasta la altura que alcanzaban las surgentes, de tal manera que el peso de la columna por unidad de área de su base equilibra la presión del agua que puja por salir, y así actúa como un tapón que interrumpe dichas surgentes. De esta manera, la altura alcanzada por el agua sobre los tubos verticales provee una medida de la presión estática del líquido respecto de la atmosférica (presión manométrica).

Figura 1. Líquido en reposo

Liquido en movimiento

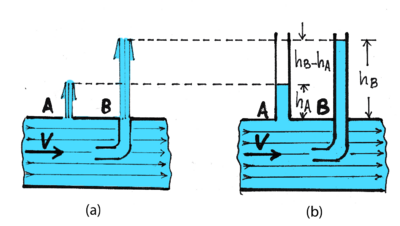
Si ahora el agua en el conducto se mueve de izquierda a derecha con una velocidad V como muestran las Figuras 2, el resultado de nuestro experimento es diferente: la altura de la surgente A ( [math]\displaystyle{ h_A }[/math] ), que continúa indicando la presión estática, es superada por la altura de la surgente B ( [math]\displaystyle{ h_B }[/math] ). donde el impulso del agua en movimiento entrando en el tubo curvado contra la corriente agrega una contribución dinámica a la presión de salida del agua.

Figura 2. Líquido en movimiento

No es difícil probar que la altura adicional ([math]\displaystyle{ h_A-h_B }[/math] ) del agua en el tubo B por encima del A es la misma que la alcanzada por un cuerpo lanzado hacia arriba con la velocidad V del líquido, esto es:

[math]\displaystyle{ h_A-h_B=\frac{V^2}{2\,g} }[/math] , Ecuación (1)

donde g es la aceleración de la gravedad terrestre (g=9.8 m/[math]\displaystyle{ seg^2} }[/math]). Así, disponemos de un método muy simple para medir la velocidad de un líquido en un conducto a partir de la medida de la diferencia de alturas que alcanza el líquido en un par de tubos insertados en dicho conducto! Le voilà!, ésto es justamente lo que se le ocurrió a Monsieur Pitot en 1732.

---

Datos biográficos: Henri Pitot (1695-1771)

Fue un físico e ingeniero hidráulico francés. Fue militar y estudió matemáticas en forma autodidacta. En 1723 fue nombrado asistente del famoso físico Réaumur, y en 1724 ingresó a la Academia Real de Ciencias francesa. Inventó el tubo que lleva su nombre, que permite calcular la velocidad de un caudal, anunciándolo como instrumento de medida de la velocidad de un flujo, algo que demostró al medir la velocidad del Río Sena que atraviesa la ciudad de Paris. Instalando su instrumento en un velero con el que surcó dicho río, también demostró su utilidad para medir la velocidad de un navío. Se le nombró ingeniero jefe de los estados del Languedoc, construyendo el acueducto de Saint-Climent, Francia. También acometió la desecación de pantanos, la construcción de puentes y saneamientos en las ciudades del Languedoc.

Determinación de la velocidad

Para poder determinar la velocidad [math]\displaystyle{ V }[/math] de un líquido a partir de otras medidas más prácticas que la original de Pitot, esto es la altura alcanzada por el mismo líquido en los tubos recto y curvado de la Figura 2b, notemos que las presiones (fuerza por unidad de área) estática ([math]\displaystyle{ P_s }[/math]) y total ([math]\displaystyle{ P_t }[/math]) vienen dadas por el peso de la columna de líquido en la base de los respectivos tubos, dividido por el área transversal (a) de dichos tubos. Esto es:

[math]\displaystyle{ P_{s}=\frac{\rho g h_A a}{a}=\rho g h_A \;\;\; \mathrm{y} \;\;\; P_{t}=\rho g h_B }[/math]

donde [math]\displaystyle{ \rho }[/math] es la densidad del líquido (masa por unidad de volumen) y [math]\displaystyle{ g }[/math] la aceleración de la gravedad. Así, multiplicando ambos miembros de la Ecuación (1) por [math]\displaystyle{ \rho\,g }[/math], resulta:

[math]\displaystyle{ P_{t}-P_{s}=\frac{1}{2}\rho V^2 \Rightarrow }[/math] [math]\displaystyle{ V=\sqrt{2\frac{P_t-P_s}{\rho}} }[/math], Ecuación (2)

de donde se puede despejar [math]\displaystyle{ V }[/math]:

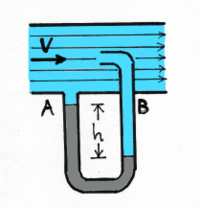
De este modo, midiendo la diferencia de presión [math]\displaystyle{ P_d = P_t - P_s }[/math] por cualquier medio y conociendo la densidad [math]\displaystyle{ \rho }[/math] del líquido, la Ecuación (2) nos permite determinar la velocidad [math]\displaystyle{ V }[/math] del mismo. El tubo original de Pitot presenta tres inconvenientes para su aplicación práctica: 1) Requiere de dos medidas, una la presión estática [math]\displaystyle{ P_s }[/math] del fluido, la otra la presión total [math]\displaystyle{ P_t }[/math] (estática + dinámica), para de allí derivar la presión dinámica [math]\displaystyle{ P_d }[/math] por diferencia. 2) Emplea como líquido manométrico el agua, que por su bajo peso específico requiere longitudes de tubos excesivos para medir las presiones usualmente encontradas en la práctica (Pitot usó en sus experimentos tubos de alrededor de 1.80 m de largo!) 3) Se aplica solamente a líquidos: en la época de Pitot aún no se contemplaban aplicaciones a la medición de corrientes de gases en general y de aire, en particular (aerodinámica). Estos inconvenientes fueron superados por el físico alemán Ludwig Prandtl (1875–1953), mediante el diseño del tubo que lleva su nombre. El tubo de Prandtl combina en un mismo instrumento ambas medidas de presión. Estas medidas son comparadas en el tubo empleando un líquido manométrico como el Hg que posee una densidad 13.6 veces mayor que la del agua, lo que reduce sensiblemente las dimensiones del instrumento. Un esquema del tubo se muestra en la Figura 3.

Figura 3. Esquema de un tubo de Prandtl. El desnivel h entre las ramas del líquido manométrico (en gris) indica la presión dinámica.

Datos biográficos: Ludwig Prandtl (1875–1953)

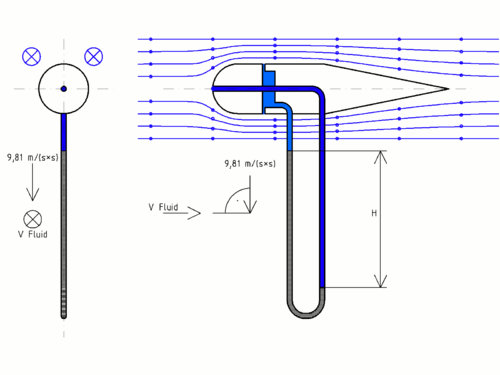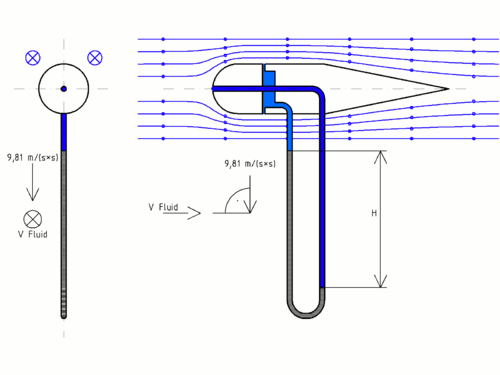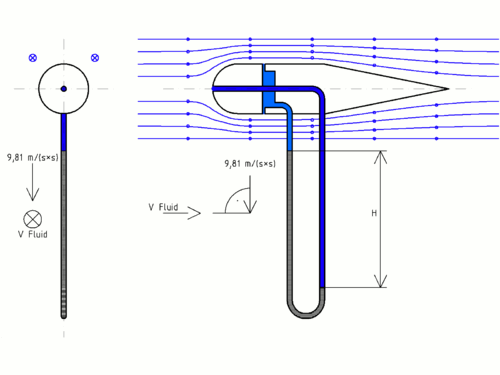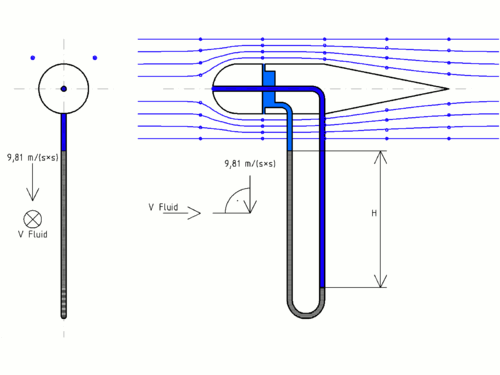
Fue un físico alemán que realizó importantes trabajos pioneros en el campo de la aerodinámica, y durante la década de 1920 desarrolló la base matemática que da sustento a los principios fundamentales de la aerodinámica subsónica. En sus estudios identificó la capa límite, y elaboró la teoría de la línea sustentadora para alas esbeltas. El número de Prandtl, que desempeña un importante papel en el análisis de problemas de fluidos, ha sido nombrado en su honor. También se destacan sus trabajos en mecánica de sólidos y estructural, en particular su contribución a la teoría de la torsión mecánica, la teoría de membranas, la capacidad portante de los terrenos y sus aplicaciones al diseño de cimentaciones, además de sus aportaciones a la teoría de la plasticidad. Una animación mostrando el funcionamiento de un tubo de Prandtl diseñado para medir la velocidad de un fluido (líquido o gas) se muestra en la Figura 4.

Figura 4. Tubo de Prandtl.

Versión moderna del tubo de Pitot-Prandtl

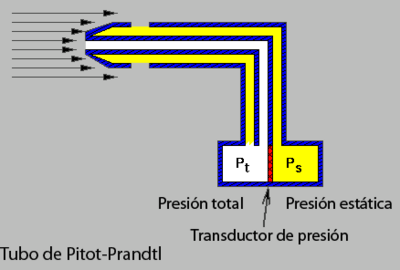
A pesar que la simple Ecuación (2) para la velocidad de la corriente se derivó tomando en cuenta un líquido (incompresible), la expresión sigue valiendo también para un gas (compresible), cuando se trata de medir velocidades pequeñas respecto a la velocidad del sonido en dicho gas (en la práctica, valores de [math]\displaystyle{ V }[/math] de hasta un 30% de la velocidad del sonido). Para velocidades mayores, la ecuación debe ser corregida. Actualmente, ya no se usa mercurio ni se recurre a la gravedad terrestre para determinar la diferencia de presión: la misma se obtiene mediante un manómetro diferencial (transductor de presión) donde se mide eléctricamente la deformación de un diafragma que separa sendos recintos del instrumento, uno de ellos con la presión total, el otro con la presión estática. La Figura 5 muestra el esquema de un tubo de Pitot-Prandtl moderno.

Figura 5. Esquema de un tubo de Pitot-Prandtl moderno.

La Figura 6 muestra un tubo de Pitot-Prandtl instalado debajo del ala de un avión, para la medida de su velocidad respecto al aire.

Figura 6. Uso del tubo de Pitot en una aeronave.

Además de las señaladas, el tubo de Pitot-Prandtl tiene diversas aplicaciones, entre ellas en Meteorología como anemómetro (Figura 7) y hasta en autos de carrera (Figura 8).

Figura 7. Anemómetro basado en el tubo de Pitot.

Figura 8. Tubo de Pitot en una Ferrari de F1.