Diferencia entre revisiones de «Teoría de la Relatividad»
| Línea 61: | Línea 61: | ||
Hasta acá muy bien, pero hay un problema: El interferómetro está sobre la Tierra, por lo que se puede observar el patrón de interferencia debido a las diferentes velocidades en las dos direcciones de los brazos del interferómetro, pero no hay manera de compararlo con el patrón correspondiente al estado de reposo respecto al éter. La solución a este problema fue medir en una posición, y luego rotar el interferómetro 90º. El desplazamiento en el patrón de interferencia en esta comparación, sería el doble del que se quiere observar |
Hasta acá muy bien, pero hay un problema: El interferómetro está sobre la Tierra, por lo que se puede observar el patrón de interferencia debido a las diferentes velocidades en las dos direcciones de los brazos del interferómetro, pero no hay manera de compararlo con el patrón correspondiente al estado de reposo respecto al éter. La solución a este problema fue medir en una posición, y luego rotar el interferómetro 90º. El desplazamiento en el patrón de interferencia en esta comparación, sería el doble del que se quiere observar |
||
| − | [[Imagen:rel2.jpg|framed| |
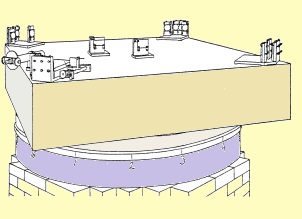
+ | [[Imagen:rel2.jpg|framed|right|100px|interferómetro utilizado por Michelson y Morley en su experimento (Wikimedia)]] |
Para el momento en que Michelson, en colaboración con Morley [16], realizó su experimento ya se había descartado la posibilidad de que la Tierra “arrastrara” al éter, como si este fuese un fluido viscoso (lo que implicaría una velocidad relativa igual a 0 en la superficie), por lo que necesariamente debía medirse una velocidad no nula del planeta respecto al éter. Sin embargo el resultado del experimento fue nulo, es decir, no se detectó movimiento de la Tierra respecto al éter. |
Para el momento en que Michelson, en colaboración con Morley [16], realizó su experimento ya se había descartado la posibilidad de que la Tierra “arrastrara” al éter, como si este fuese un fluido viscoso (lo que implicaría una velocidad relativa igual a 0 en la superficie), por lo que necesariamente debía medirse una velocidad no nula del planeta respecto al éter. Sin embargo el resultado del experimento fue nulo, es decir, no se detectó movimiento de la Tierra respecto al éter. |
||
Revisión del 19:01 9 oct 2013
En 1905, Albert Einstein [1] publica una teoría controversial, con la que se proponía mostrar una nueva forma de entender las leyes de la física. Para darnos una idea de que se trata, debemos retrotraernos al nacimiento de lo que hoy llamamos física. En el siglo XVI, Isaac Newton [2] se propone encontrar una explicación común al movimiento de los cuerpos celestes y al de los objetos que observamos en la tierra. El precursor de estas investigaciones había sido Galileo [3].Para eso formulará una serie de hipótesis (las tres leyes de la mecánica) que de alguna manera representan más que una descripción del mundo físico, un método para pensarlo. A partir de esas tres leyes, de las observaciones astronómicas y de experimentos de laboratorio encontrará una ley simple (la ley de la gravitación universal) que permitirá explicar todos esos fenómenos.
El principio de relatividad en la mecánica newtoniana
Por el Lic. Nicolás Gigena
En su famosa obra Principia [1] Newton presenta sus 3 leyes del movimiento y la ley de gravitación universal, sentando las bases de la mecánica clásica. Es también en sus Principia donde Newton postula el carácter absoluto del espacio y el tiempo. Esto es lo que decía sobre el espacio:
El espacio absoluto, por su propia naturaleza y sin relación alguna con nada externo, permanece similar e inmóvil. El espacio relativo es una dimensión o medida movible de los espacios absolutos que nuestros sentidos determinan de acuerdo con su posición con respecto a los cuerpos y que por lo común se toma como espacio inmóvil; tal es la dimensión de un espacio subterráneo, aéreo o celeste, determinada través de su posición con respecto a la Tierra. El espacio absoluto y el relativo son iguales en forma y magnitud, pero no siempre coinciden numéricamente, un espacio cualquiera de nuestro aire, que relativamente a la Tierra y con respecto a la Tierra permanece siempre igual, en un momento dado ocupa una cierta parte del espacio absoluto por el que atraviesa el aire; en otra parte ocupará otra parte distinta del mismo y así entendido su sentido absoluto, irá modificándose continuamente.
Y otro tanto sobre el tiempo:
El tiempo absoluto, verdadero y matemático, en sí mismo por su propia naturaleza, fluye de una manera ecuable y sin relación alguna con nada externo y, se conoce también con el nombre de duración; el tiempo relativo, aparente y común es una medida sensible y externa (ya sea exacta e inecuable) de la duración por medio del movimiento, y se utiliza corrientemente en lugar del tiempo verdadero; ejemplo de ello son la hora, el día, el mes el año. Lo que dice Newton es que espacio y tiempo son cosas que existen por sí mismas, haciendo de escenario en el que tienen lugar los fenómenos físicos. Sin embargo estos entes no pueden ser percibidos si no es a través de posiciones relativas y movimiento. Así, cuando medimos la posición de un cuerpo respecto a otro, según Newton, estamos midiendo cuánto espacio hay entre esos 2 cuerpos. Cuando comparamos una sucesión de eventos con, por ejemplo, el movimiento de un péndulo, estamos midiendo cuánto tiempo transcurre entre el primer evento y el último.
Puede no resultar obvio, pero la existencia de un espacio y un tiempo absolutos implica que los intervalos de tiempo y espacio entre dos eventos dados son los mismos para todos los observadores en movimiento relativo uniforme, y por lo tanto, que eventos que son simultáneos para un dado observador también han de serlo para todos los demás. Ahora bien, estas consecuencias están en acuerdo con nuestra experiencia cotidiana: Nuestros relojes no parecen adelantar o atrasar por el solo hecho de estar viajando en auto, por ejemplo, ni tampoco observamos que la graduación de una regla cambie mientras la movemos de un lado a otro. Ciertamente parece razonable pensar que, si en los experimentos los relojes de todos los observadores marcan lo mismo, puede ser que estén midiendo lo mismo, a saber, el tiempo absoluto. Lo mismo valdría para el espacio absoluto. No obstante, como sabemos, este razonamiento es erróneo.
El principio de relatividad de Galileo
Por extraño que pueda parecer, el primer enunciado del principio de relatividad se remonta a los trabajos de Galileo Galilei. Basándose en los resultados de sus observaciones, en 1632 Galileo escribía en su obra Diálogos sobre los dos máximos sistemas del mundo [3]:
Encerraos con un amigo en la cabina principal bajo la cubierta de un barco grande, y llevad con vosotros moscas, mariposas, y otros pequeños animales voladores… colgad una botella que se vacíe gota a gota en un amplio recipiente colocado por debajo de la misma… haced que el barco vaya con la velocidad que queráis, siempre que el movimiento sea uniforme y no haya fluctuaciones en un sentido u otro…. Las gotas caerán… en el recipiente inferior sin desviarse a la popa, aunque el barco haya avanzado mientras las gotas están en el aire… las mariposas y las moscas seguirán su vuelo por igual hacia cada lado, y no sucederá que se concentren en la popa, como si cansaran de seguir el curso del barco…|Galileo Galilei
Lo que Galileo afirma es que, mientras el movimiento del barco sea uniforme (es decir, su velocidad respecto a tierra sea constante), los resultados de los experimentos realizados en el barco deberían coincidir con los de aquellos realizados en tierra firme. Supongamos ahora que tenemos un conjunto de “leyes” que nos permiten describir los fenómenos físicos, y predecir resultados de experimentos. Si es cierta la afirmación de Galileo entonces estas leyes deben ser las mismas en Tierra y sobre el barco, puesto que las descripciones y predicciones han de coincidir. Podemos utilizar esta idea para convertir la observación de Galileo en un principio general (principio de relatividad): Las leyes que describen los fenómenos físicos son las mismas para todos los observadores en movimiento relativo uniforme.
Pero podemos ir todavía un poco más lejos. Dado que las leyes físicas se expresan mediante ecuaciones, el principio de relatividad implicaría que estas ecuaciones deben ser las mismas para todos los observadores en movimiento relativo uniforme. Veamos cómo se expresa esto matemáticamente:
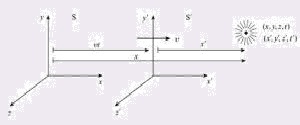
Imaginemos dos observadores S y S’ en movimiento relativo con velocidad v, esto es, S’ se mueve respecto a S con velocidad v. Estos observadores miden la posición de un objeto usando coordenadas x y x’ respectivamente. Dado que suponemos tiempo absoluto, una vez sincronizados (S y S’ están en el mismo lugar cuando empiezan a medir el tiempo) los relojes de S y S’ marcan siempre lo mismo, lo que expresamos escribiendo t=t’. ¿Cómo se relacionan las coordenadas x y x’?
Como se ve en la figura, siempre podemos escribir a la distancia del objeto a S (el valor de x) como la suma entre la distancia entre S y S’ y la distancia del objeto a S’ (el valor de x’). Además, sabemos que S’ se mueve con velocidad v respecto a S, por lo que en cualquier instante t la distancia de S a S’ es vt. Podemos escribir entonces
<\math> x = x’ + v.t ó x’= x - v.t <\math>
Esta regla para “pasar” de las coordenadas de S a las de S’ y viceversa se conoce como transformación de coordenadas´´, y nos permite comparar lo que “ven” distintos observadores en movimiento relativo uniforme. Lo que dice el principio de relatividad, entonces, es que las ecuaciones deben mantener su forma cuando cambiamos de x a x’. La segunda ley de Newton [4], por ejemplo, es la misma para todos los observadores en movimiento relativo uniforme. Es decir, si vale F=m.a para el observador S, entonces también vale F’=m.a’ para S’, si las coordenadas de S y S’ se relacionan mediante la transformación de coordenadas que definimos. La mecánica clásica es compatible con el principio de relatividad, es decir, las ecuaciones de movimiento de los sistemas mecánicos son invariantes frente a estas transformaciones de coordenadas.
En este punto conviene llamar la atención sobre algo que puede haber pasado inadvertido. Para llevar el principio enunciado por Galileo al ámbito de las ecuaciones tuvimos que establecer las transformaciones de coordenadas (transformaciones de Galileo, de ahora en más), y estas dependen del tiempo absoluto postulado por Newton. Si cambiáramos nuestra forma de entender el tiempo y el espacio (como haría Einstein al formular su teoría) estas transformaciones serían diferentes, y las ecuaciones que describen las leyes físicas deberían adaptarse a estas nuevas transformaciones, si se pretende que sean las mismas para todos los observadores en movimiento relativo uniforme. La posibilidad del reposo absoluto
Gracias a los experimentos realizados por Young [5] y Fresnel [6], entre otros, durante la primera mitad del siglo XIX los físicos llegaron a convencerse de la naturaleza ondulatoria de la luz. En analogía con las ondas mecánicas, que consisten en vibraciones de un medio elástico, se propuso un medio para la propagación de las ondas electromagnéticas: El éter luminífero. Este medio debía ser, por fuerza, algo especial. Debía tratarse de un sólido elástico y no dispersivo, de manera que la propagación de la luz pudiese entenderse como el resto de las ondas mecánicas, pero también debía tener la capacidad de penetrar otros medios materiales interactuando con estos en alguna manera, de forma que fuera posible explicar la propagación de la luz en medios como el aire, la luz y el vidrio y sus respectivos índices de refracción [7]. Más importante aún, dado que el éter debía llenar todo el espacio para hacer posible la propagación de la luz, éste debía estar en reposo respecto al espacio absoluto. Podría decirse que el éter era la materialización del espacio absoluto propuesto por Newton.
En 1873 Maxwell [8] publica su conocida obra, A treatise on electricity and magnetism, en la que presenta una teoría que unifica los fenómenos eléctricos y magnéticos. Una predicción de esta teoría es la existencia de ondas electromagnéticas, esto es, en ausencia de fuentes de carga [9] y corriente [10] las ecuaciones de Maxwell [11] llevan a que los campos eléctrico y magnético deben ser solución de una ecuación de ondas [12]. Cuando Maxwell encontró estas soluciones notó que la velocidad a la que deberían propagarse estas ondas electromagnéticas, según la teoría, era muy similar a la velocidad medida para la propagación de la luz, por lo que conjeturó que la luz era un caso especial de onda electromagnética. Esta conjetura fue posteriormente confirmada por los experimentos realizados por Hertz [13]. Así la óptica quedaba integrada como parte del electromagnetismo, y el éter luminífero pasó a coincidir con el medio que Maxwell postulara para la propagación de las ondas electromagnéticas. Las consecuencias de esto no son menores: La existencia de las ondas electromagnéticas llevó a proponer la existencia de un medio en el que los campos “viven”, lo que implica que la teoría de Maxwell consiste en un conjunto de leyes que describe los fenómenos electromagnéticos para observadores en reposo respecto a este medio, por lo que el principio de relatividad deja de valer en el reino de los fenómenos electromagnéticos. La identificación de dicho medio con el éter luminífero implica que el sistema de referencia en el que vale la teoría electromagnética está en reposo absoluto.
La teoría de Maxwell fue muy exitosa explicando fenómenos electromagnéticos conocidos, y además proporcionó predicciones que luego fueron confirmadas experimentalmente. Los problemas empezaron cuando los físicos se propusieron conocer cuál era el estado de movimiento de la Tierra respecto al éter. Resolver este problema era de importancia porque, supuesta la existencia del éter, es claro que las ecuaciones de Maxwell permiten conocer los campos eléctrico y magnético en un sistema de referencia en reposo respecto al éter, y para saber qué es lo que ve un observador en movimiento respecto al mismo es necesario conocer su velocidad relativa (de la que dependen las transformaciones de Galileo). Dicho de otra manera: la velocidad de la luz que predice la teoría de Maxwell sería solo la que mediría un observador en reposo respecto al éter, y otros observadores en movimiento relativo medirían otra, tal y como pasa con las ondas mecánicas. Entre los varios intentos de resolver esta cuestión destaca el experimento de Michelson y Morley.
El experimento de Michelson y Morley
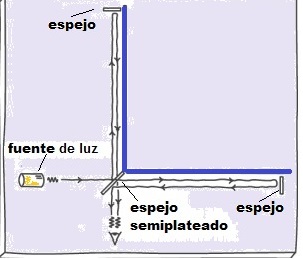
Michelson [14] diseñó un experimento para determinar la velocidad relativa de la Tierra respecto al éter. La idea es relativamente sencilla: Tenemos el éter llenando todo el espacio y la tierra moviéndose a través de este en alguna dirección dada. Podemos imaginarnos que, mediante algún dispositivo, nos es posible generar dos pulsos luminosos que se propagan en direcciones distintas: Uno de ellos en la dirección del movimiento de la Tierra respecto al éter, y el otro en dirección perpendicular a este. En un sistema de referencia en reposo respecto del éter los dos pulsos viajarían a la misma velocidad, esos casi 3×10^8 m/s (300.000km/s), que predice la teoría de Maxwell. Pero en un sistema en reposo respecto a la Tierra las velocidades serían distintas, debido a que las transformaciones de Galileo dicen que las velocidades se suman. Así, el pulso luminoso que se propaga en la dirección normal al movimiento de la Tierra respecto al éter debería propagarse a la misma velocidad que en el éter (dado que la velocidad relativa es nula), pero el otro pulso debería propagarse a una velocidad c’ un poco menor, resultado de la diferencia entre la velocidad medida en el éter y la velocidad relativa entre la Tierra y dicho medio, es decir c’= (3×10^8 – v) m/s. Una medida de la velocidad de estos pulsos permitiría, entonces, conocer la velocidad con la que la Tierra se mueve en el éter. Como muchas ideas simples, llevar esto a un dispositivo real resultó complicado. ¿Cómo generar dos pulsos de luz simultáneos, y además medir su velocidad? La solución de Michelson llegó con la construcción de su interferómetro, que convierte el problema de los pulsos de luz en un problema de interferencia [15] . Este es un esquema simplificado que muestra cómo funciona.
La fuente emite un haz de luz monocromática que al llegar al espejo semiplateado se divide en dos haces perpendiculares. Estos haces se reflejan en espejos diferentes y vuelven hacia el espejo semiplateado para reflejarse nuevamente en dirección hacia una pantalla (representada por un ojo en la figura) en la que se forma un patrón de interferencia, debido a una diferencia de fase entre los dos haces. La idea entonces era la siguiente: Mientras el interferómetro estuviese en reposo respecto al éter, el patrón de interferencia sería siempre el mismo. Si, en cambio, el interferómetro se moviera respecto al éter en dirección paralela a alguno de sus brazos, entonces para un observador en reposo respecto al interferómetro la velocidad de la luz tendría un valor diferente en esa dirección. Debido a este cambio en la velocidad en una sola de las direcciones, la fase relativa de los haces de luz en el espejo semiplateado también cambia, provocando un patrón de interferencia diferente en la pantalla.
Hasta acá muy bien, pero hay un problema: El interferómetro está sobre la Tierra, por lo que se puede observar el patrón de interferencia debido a las diferentes velocidades en las dos direcciones de los brazos del interferómetro, pero no hay manera de compararlo con el patrón correspondiente al estado de reposo respecto al éter. La solución a este problema fue medir en una posición, y luego rotar el interferómetro 90º. El desplazamiento en el patrón de interferencia en esta comparación, sería el doble del que se quiere observar
Para el momento en que Michelson, en colaboración con Morley [16], realizó su experimento ya se había descartado la posibilidad de que la Tierra “arrastrara” al éter, como si este fuese un fluido viscoso (lo que implicaría una velocidad relativa igual a 0 en la superficie), por lo que necesariamente debía medirse una velocidad no nula del planeta respecto al éter. Sin embargo el resultado del experimento fue nulo, es decir, no se detectó movimiento de la Tierra respecto al éter.
¿Qué falló?
La interpretación rápida de los resultados de este experimento sería: El desplazamiento observado es nulo, luego la velocidad relativa de la Tierra respecto al éter es nula. Pero esta interpretación ya en ese entonces se sabía imposible. Una posible explicación a este resultado fue provista por Lorentz [17] en 1892, quien introdujo como hipótesis que los cuerpos en movimiento relativo respecto al éter deberían contraerse en un factor dependiente de la velocidad de desplazamiento. La hipótesis se introduce ad hoc: Lorentz compensa la variación que debería observarse en la velocidad de la luz con un acortamiento en la longitud del brazo en la dirección de movimiento, de manera que el efecto neto del desplazamiento a través del éter sea nulo.
Si bien la solución propuesta no resulta muy agradable (lo sería si la contracción propuesta pudiese deducirse en lugar de introducirse a la fuerza) la teoría de Lorentz resultó exitosa, puesto que eliminaba las inconsistencias que surgían de los resultados nulos en los experimentos como el de Michelson y Morley, que intentaban medir el desplazamiento respecto al éter.
Restitución del principio de relatividad
El primer artículo de Einstein sobre la teoría de la relatividad fue publicado en 1905, bajo el título Sobre la electrodinámica de cuerpos en movimiento. La siguiente cita es de la introducción del artículo:
Se sabe que cuando la electrodinámica de Maxwell – tal como se suele entender actualmente – se aplica a cuerpos en movimiento, aparecen asimetrías que no parecen estar en correspondencia con los fenómenos observados. Pensemos, por ejemplo, en la interacción electrodinámica entre un imán y un conductor. En este caso, el fenómeno que se observa depende solamente del movimiento relativo entre el conductor y el imán, mientras que de acuerdo a la interpretación común se deben distinguir claramente dos casos muy diferentes, dependiendo de cuál de los dos cuerpos se mueva. Si se mueve el imán mientras que el conductor se encuentra en reposo, alrededor del imán aparece un campo eléctrico con cierto valor para su energía. Este campo eléctrico genera una corriente en el lugar donde se encuentre el conductor. Pero si el imán está en reposo y el conductor se mueve, alrededor del imán no aparece ningún campo eléctrico sino que en el conductor se produce una fuerza electromotriz que en sí no corresponde a ninguna energía pero da lugar a corrientes eléctricas que coinciden en magnitud y dirección con las del primer caso, suponiendo que el movimiento relativo es igual en cada uno de los casos bajo consideración.
Otros ejemplos de esta índole así como los intentos infructuosos para constatar un movimiento de la Tierra con respecto al “medio de propagación de la luz” permiten suponer que no solamente en mecánica sino también en electrodinámica ninguna de las propiedades de los fenómenos corresponde al concepto de reposo absoluto. Lo que parece molestar a Einstein es que un fenómeno único desde el punto de vista de la mecánica tenga dos descripciones diferentes en el electromagnetismo. Dicho de otra manera, que el principio de relatividad sea válido en el ámbito de la mecánica, pero no así en el reino de los fenómenos electromagnéticos. Ahora bien, esta asimetría, por sí misma, no necesariamente constituye un problema. Recordemos que los campos electromagnéticos viven en el éter, y que la teoría desarrollada por Maxwell consiste en un conjunto de leyes que describen los fenómenos electromagnéticos respecto a un observador en reposo respecto al éter, es decir, en reposo absoluto. La asimetría de la que habla Einstein, entonces, no es más que una consecuencia de este hecho. El principio de relatividad deja de valer en el electromagnetismo porque, a diferencia de lo que pasa dentro de la mecánica, los fenómenos electromagnéticos sí distinguen el reposo absoluto. Matemáticamente, además, esto se refleja en el hecho de que las ecuaciones del electromagnetismo no conservan su forma frente a las transformaciones de Galileo. Todo parece ser consistente. Sin embargo, como deja entrever Einstein en el segundo párrafo, esta explicación puede objetarse. Si es cierto que estas asimetrías quedan explicadas por la capacidad del electromagnetismo de distinguir el reposo absoluto: ¿Por qué fallan los experimentos que intentan medir desplazamiento respecto al éter?
Einstein propone una teoría alternativa a la de Lorentz partiendo de 2 hipótesis: 1) En todos los sistemas de coordenadas en los que tienen validez las ecuaciones de la mecánica, tienen también validez las mismas leyes de la electrodinámica. 2) La luz puede propagarse en el vacío, y lo hace de manera tal que su velocidad de propagación no depende de la velocidad de la fuente.
En la primera hipótesis se extiende el principio de relatividad de Galileo al electromagnetismo: Todos los observadores en movimiento relativo uniforme describen los fenómenos de la misma manera, es decir, con las mismas ecuaciones. Esto implica que las ecuaciones deben tener una forma invariante frente a transformaciones de coordenadas. La hipótesis en 2) sobre la velocidad de la luz es, en realidad, una característica común a todos los fenómenos ondulatorios, pero en este caso hay una diferencia importante. En el caso de las ondas mecánicas la velocidad de propagación es independiente del movimiento de la fuente porque está determinada exclusivamente por las propiedades elásticas del medio. Pero en el caso de la luz, la independencia de la fuente combinada con la propagación en el vacío llevan a un resultado poco intuitivo: La velocidad de la luz es la misma para todos los observadores en movimiento relativo uniforme.
Al sacar al éter del escenario Einstein enfrenta el problema de fondo, que es la incompatibilidad de las transformaciones de Galileo con la teoría electromagnética. En efecto, si el principio de relatividad es válido y la velocidad de la luz es la misma para todos los observadores en movimiento relativo uniforme, entonces la teoría electromagnética es correcta, y las transformaciones de Galileo no lo son. Las transformaciones correctas no son otras que las obtenidas por Lorentz en su intento por explicar el resultado nulo del experimento de Michelson y Morley. La genialidad del trabajo de Einstein radica en mostrar que estas transformaciones surgen naturalmente de sus dos postulados, y de un análisis crítico de lo que se entiende por tiempo y espacio, que requiere el abandono de los absolutos newtonianos.
Debug data: