Diferencia entre revisiones de «El efecto Coriolis»
| (No se muestran 4 ediciones intermedias del mismo usuario) | |||
| Línea 4: | Línea 4: | ||
En el instante t=0 el cañón dispara un proyectil. En el sistema de referencia inercial la situación es muy simple: Como no hay acciones externas el proyectil va a mantener su estado de movimiento (esta es la primera ley de Newton), siguiendo una trayectoria recta. En el sistema de referencia en rotación el movimiento es un poquito más complicado pues esta trayectoria recta va a aparecer curva, lo que implica que, para este observador, la bala aparecerá como acelerada. Si este observador utilizara las leyes de Newton se vería obligado a concluir que una fuerza de origen desconocido actúa sobre el proyectil, causando la curvatura en la trayectoria. Esta fuerza es ficticia, puesto que surge de utilizar las leyes de Newton en un sistema de referencia no inercial. |
En el instante t=0 el cañón dispara un proyectil. En el sistema de referencia inercial la situación es muy simple: Como no hay acciones externas el proyectil va a mantener su estado de movimiento (esta es la primera ley de Newton), siguiendo una trayectoria recta. En el sistema de referencia en rotación el movimiento es un poquito más complicado pues esta trayectoria recta va a aparecer curva, lo que implica que, para este observador, la bala aparecerá como acelerada. Si este observador utilizara las leyes de Newton se vería obligado a concluir que una fuerza de origen desconocido actúa sobre el proyectil, causando la curvatura en la trayectoria. Esta fuerza es ficticia, puesto que surge de utilizar las leyes de Newton en un sistema de referencia no inercial. |
||
| − | En 1835 el ingeniero Gaspard-Gustave de Coriolis (https://es.wikipedia.org/wiki/Gaspard_Coriolis) se dedicó a estudiar el movimiento de cuerpos en sistemas de referencia en rotación y encontró que esta fuerza ficticia puede descomponerse en dos contribuciones. La primera es la fuerza centrífuga por todos conocida; esa fuerza que sentimos que nos empuja contra la puerta cuando vamos |
+ | En 1835 el ingeniero Gaspard-Gustave de Coriolis (https://es.wikipedia.org/wiki/Gaspard_Coriolis) se dedicó a estudiar el movimiento de cuerpos en sistemas de referencia en rotación y encontró que esta fuerza ficticia puede descomponerse en dos contribuciones. La primera es la fuerza centrífuga por todos conocida; esa fuerza que sentimos que nos empuja contra la puerta cuando vamos a lo largo de una curva en el auto. La otra contribución es hoy conocida como fuerza de Coriolis, pero en su momento él la llamó fuerza centrífuga compuesta, y determinó que depende tanto de la velocidad v de la bala como de la velocidad angular ω entre los sistemas. Esta aceleración de Coriolis es responsable por la curvatura en la trayectoria del proyectil. |
| − | [[Imagen:tierra.jpg| |
+ | [[Imagen:tierra.jpg|260px|left]] |
MOVIMIENTO RELATIVO A LA TIERRA |
MOVIMIENTO RELATIVO A LA TIERRA |
||
| Línea 17: | Línea 17: | ||
Supongamos que el cañón está en algún punto de latitud λ1 en el hemisferio norte y dispara el proyectil hacia el Norte, como se ve en el dibujo de abajo. Como el cañón está fijo a la superficie de la Tierra vamos a ver que el proyectil tiene no solo velocidad en dirección hacía el polo sino también una componente de velocidad hacia el Este igual a la velocidad con la que vemos moverse a la superficie, debido a la inercia. En otras palabras, vamos a ver que además de ir hacia el Norte el proyectil sigue rotando con la Tierra. Para saber qué trayectoria va a describir el proyectil podemos considerar su momento angular (https://es.wikipedia.org/wiki/Momento_angular). Lo importante para nosotros sobre esta cantidad es que implica que el producto entre la velocidad de rotación ω del proyectil y su distancia al eje de la Tierra r, debe mantenerse constante. Ahora bien, como la distancia desde la superficie al eje de la Tierra disminuye al aumentar la latitud, como se aprecia en el dibujo, en su camino en dirección Norte el proyectil va a ir acercándose más y más al eje, lo que implica que la velocidad a la que rota debe aumentar para mantener constante el producto ω.r, y por lo tanto debe adelantar a la Tierra en su movimiento de rotación. Como resultado, vamos a ver que el proyectil no solo se desplaza respecto a la superficie en dirección Norte, sino también en dirección Este. Si por, por el contrario, el disparo fuese hacia el Sur, entonces en su viaje el proyectil se va a alejar del eje, y como resultado su velocidad de rotación va a disminuir, atrasando respecto de la superficie de la Tierra, y aterrizando en un lugar más al Oeste del inicial. |
Supongamos que el cañón está en algún punto de latitud λ1 en el hemisferio norte y dispara el proyectil hacia el Norte, como se ve en el dibujo de abajo. Como el cañón está fijo a la superficie de la Tierra vamos a ver que el proyectil tiene no solo velocidad en dirección hacía el polo sino también una componente de velocidad hacia el Este igual a la velocidad con la que vemos moverse a la superficie, debido a la inercia. En otras palabras, vamos a ver que además de ir hacia el Norte el proyectil sigue rotando con la Tierra. Para saber qué trayectoria va a describir el proyectil podemos considerar su momento angular (https://es.wikipedia.org/wiki/Momento_angular). Lo importante para nosotros sobre esta cantidad es que implica que el producto entre la velocidad de rotación ω del proyectil y su distancia al eje de la Tierra r, debe mantenerse constante. Ahora bien, como la distancia desde la superficie al eje de la Tierra disminuye al aumentar la latitud, como se aprecia en el dibujo, en su camino en dirección Norte el proyectil va a ir acercándose más y más al eje, lo que implica que la velocidad a la que rota debe aumentar para mantener constante el producto ω.r, y por lo tanto debe adelantar a la Tierra en su movimiento de rotación. Como resultado, vamos a ver que el proyectil no solo se desplaza respecto a la superficie en dirección Norte, sino también en dirección Este. Si por, por el contrario, el disparo fuese hacia el Sur, entonces en su viaje el proyectil se va a alejar del eje, y como resultado su velocidad de rotación va a disminuir, atrasando respecto de la superficie de la Tierra, y aterrizando en un lugar más al Oeste del inicial. |
||
| − | [[Imagen:figcr2.jpg| |
+ | [[Imagen:figcr2.jpg|360px|left]] |
Un observador situado sobre la superficie, evidentemente, debe observar el mismo desplazamiento del proyectil respecto al suelo. Pero como no puede percibir la rotación de la Tierra no puede hacer el mismo análisis que nosotros. Este observador nota el mismo cambio en la velocidad del proyectil relativa al suelo, y por las leyes de Newton deduce que una fuerza debe estar actuando sobre éste, aunque su origen es desconocido. Ésta es la fuerza de Coriolis. |
Un observador situado sobre la superficie, evidentemente, debe observar el mismo desplazamiento del proyectil respecto al suelo. Pero como no puede percibir la rotación de la Tierra no puede hacer el mismo análisis que nosotros. Este observador nota el mismo cambio en la velocidad del proyectil relativa al suelo, y por las leyes de Newton deduce que una fuerza debe estar actuando sobre éste, aunque su origen es desconocido. Ésta es la fuerza de Coriolis. |
||
| Línea 27: | Línea 27: | ||
| − | [[Imagen:figcr3.jpg| |
+ | [[Imagen:figcr3.jpg|360px|left]] |
El resultado entonces es que el proyectil va a alejarse en dirección Sur si estamos en el hemisferio norte, y en dirección Norte si estamos en el hemisferio sur. La trayectoria, por lo tanto, se desvía hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur. Si, por el contrario, disparamos hacia el oeste, la velocidad v se va a restar de la velocidad de rotación de la Tierra; la velocidad neta va a ser menor y por lo tanto una parte menor del peso es necesaria para confinar el proyectil a la superficie. Como ahora la gravedad hace más fuerza de la necesaria en dirección hacia el eje de rotación y no hay otra fuerza que la compense en dirección paralela al piso, el resultado es que el proyectil va a acelerar hacia el Norte (hacia la derecha) en el hemisferio norte y hacia el Sur (hacia la izquierda) en el hemisferio sur. |
El resultado entonces es que el proyectil va a alejarse en dirección Sur si estamos en el hemisferio norte, y en dirección Norte si estamos en el hemisferio sur. La trayectoria, por lo tanto, se desvía hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur. Si, por el contrario, disparamos hacia el oeste, la velocidad v se va a restar de la velocidad de rotación de la Tierra; la velocidad neta va a ser menor y por lo tanto una parte menor del peso es necesaria para confinar el proyectil a la superficie. Como ahora la gravedad hace más fuerza de la necesaria en dirección hacia el eje de rotación y no hay otra fuerza que la compense en dirección paralela al piso, el resultado es que el proyectil va a acelerar hacia el Norte (hacia la derecha) en el hemisferio norte y hacia el Sur (hacia la izquierda) en el hemisferio sur. |
||
| Línea 38: | Línea 38: | ||
La aceleración de Coriolis tiene gran importancia para la meteorología, pues es un efecto con una fuerte incidencia en el movimiento de grandes masas de aire. La siguiente imagen, tomada por el satélite METEOSAT-7 (https://es.wikipedia.org/wiki/Meteosat) EN 2011, representa una espectacular manifestación del efecto Coriolis |
La aceleración de Coriolis tiene gran importancia para la meteorología, pues es un efecto con una fuerte incidencia en el movimiento de grandes masas de aire. La siguiente imagen, tomada por el satélite METEOSAT-7 (https://es.wikipedia.org/wiki/Meteosat) EN 2011, representa una espectacular manifestación del efecto Coriolis |
||
| − | [[Imagen:figcr4.jpg| |
+ | [[Imagen:figcr4.jpg|450px|left]] |
| + | |||
En la imagen, prácticamente sobre el mismo meridiano se muestran dos ciclones ocurriendo simultáneamente: Thane, Al norte del Ecuador y sobre la costa India, y Benilde, al sur del Ecuador y sobre el océano Índico. Debido a que están en diferentes hemisferios estos ciclones rotan en sentido contrario. El ciclón Benilde rota en sentido horario mientras Thane rota en sentido antihorario. |
En la imagen, prácticamente sobre el mismo meridiano se muestran dos ciclones ocurriendo simultáneamente: Thane, Al norte del Ecuador y sobre la costa India, y Benilde, al sur del Ecuador y sobre el océano Índico. Debido a que están en diferentes hemisferios estos ciclones rotan en sentido contrario. El ciclón Benilde rota en sentido horario mientras Thane rota en sentido antihorario. |
||
Revisión actual - 19:55 9 mar 2017
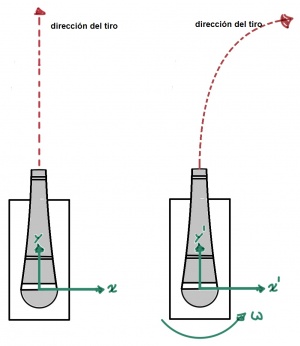
El efecto Coriolis es una consecuencia de estudiar el movimiento de los cuerpos desde un sistema de referencia particular. Los sistemas de referencia pueden clasificarse en "inerciales" y "no inerciales", y la diferencia entre estas clases está en que las leyes de Newton son válidas en la primera pero no en la segunda. En particular, un sistema de referencia que rota respecto a un sistema inercial es no inercial, y es precisamente éste el caso en el que surge el efecto Coriolis. Para aclarar un poco, imaginemos un cañón en reposo en el origen de un sistema de referencia inercial K y un segundo sistema de referencia K' con el mismo origen, pero rotando respecto al primero sobre una plataforma giratoria con velocidad angular constante ω, tal como se muestra en la figura 1.
En el instante t=0 el cañón dispara un proyectil. En el sistema de referencia inercial la situación es muy simple: Como no hay acciones externas el proyectil va a mantener su estado de movimiento (esta es la primera ley de Newton), siguiendo una trayectoria recta. En el sistema de referencia en rotación el movimiento es un poquito más complicado pues esta trayectoria recta va a aparecer curva, lo que implica que, para este observador, la bala aparecerá como acelerada. Si este observador utilizara las leyes de Newton se vería obligado a concluir que una fuerza de origen desconocido actúa sobre el proyectil, causando la curvatura en la trayectoria. Esta fuerza es ficticia, puesto que surge de utilizar las leyes de Newton en un sistema de referencia no inercial.
En 1835 el ingeniero Gaspard-Gustave de Coriolis (https://es.wikipedia.org/wiki/Gaspard_Coriolis) se dedicó a estudiar el movimiento de cuerpos en sistemas de referencia en rotación y encontró que esta fuerza ficticia puede descomponerse en dos contribuciones. La primera es la fuerza centrífuga por todos conocida; esa fuerza que sentimos que nos empuja contra la puerta cuando vamos a lo largo de una curva en el auto. La otra contribución es hoy conocida como fuerza de Coriolis, pero en su momento él la llamó fuerza centrífuga compuesta, y determinó que depende tanto de la velocidad v de la bala como de la velocidad angular ω entre los sistemas. Esta aceleración de Coriolis es responsable por la curvatura en la trayectoria del proyectil.
MOVIMIENTO RELATIVO A LA TIERRA
Como la Tierra gira en torno a un eje propio un observador sobre su superficie es un observador no inercial, y por lo tanto está en la situación del observador en rotación discutido más arriba. De manera que al estudiar el movimiento de un cuerpo desde nuestro laboratorio, en reposo respecto a la Tierra, vamos a observar que su trayectoria se ve afectada por la aceleración de Coriolis.
Volvamos al cañón del ejemplo anterior. Supongamos que está sobre la superficie de la Tierra y dispara sus proyectiles en dirección horizontal. Si estamos en reposo respecto al cañón esperaríamos ver que el proyectil se aleja en línea recta hacia adelante con velocidad constante, pero no es el caso. Debido a la rotación de la Tierra vamos a encontrar que, de hecho, la trayectoria se desvía siempre hacia la derecha si estamos en el hemisferio norte, o siempre hacia la izquierda si es que estamos en el hemisferio sur. Podemos entender por qué ésta es la trayectoria del proyectil sin hacer cálculos, si en lugar de quedarnos fijos a la superficie de la Tierra nos imaginamos levitando sobre esta, de manera de percibir su rotación (o sea, si nos cambiamos a un referencial inercial). Además, como la velocidad en cualquier dirección puede descomponerse en una contribución en dirección Norte-Sur más una contribución Este-Oeste, con entender estos dos casos va a ser suficiente.
MOVIMIENTO EN DIRECCIÓN NORTE-SUR
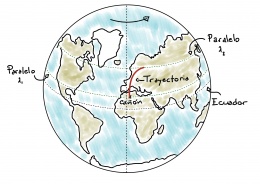
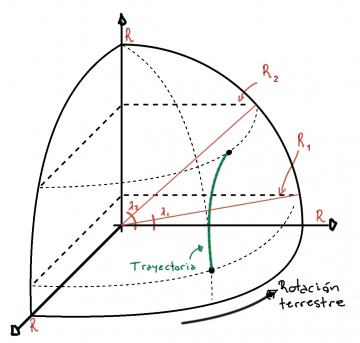
Supongamos que el cañón está en algún punto de latitud λ1 en el hemisferio norte y dispara el proyectil hacia el Norte, como se ve en el dibujo de abajo. Como el cañón está fijo a la superficie de la Tierra vamos a ver que el proyectil tiene no solo velocidad en dirección hacía el polo sino también una componente de velocidad hacia el Este igual a la velocidad con la que vemos moverse a la superficie, debido a la inercia. En otras palabras, vamos a ver que además de ir hacia el Norte el proyectil sigue rotando con la Tierra. Para saber qué trayectoria va a describir el proyectil podemos considerar su momento angular (https://es.wikipedia.org/wiki/Momento_angular). Lo importante para nosotros sobre esta cantidad es que implica que el producto entre la velocidad de rotación ω del proyectil y su distancia al eje de la Tierra r, debe mantenerse constante. Ahora bien, como la distancia desde la superficie al eje de la Tierra disminuye al aumentar la latitud, como se aprecia en el dibujo, en su camino en dirección Norte el proyectil va a ir acercándose más y más al eje, lo que implica que la velocidad a la que rota debe aumentar para mantener constante el producto ω.r, y por lo tanto debe adelantar a la Tierra en su movimiento de rotación. Como resultado, vamos a ver que el proyectil no solo se desplaza respecto a la superficie en dirección Norte, sino también en dirección Este. Si por, por el contrario, el disparo fuese hacia el Sur, entonces en su viaje el proyectil se va a alejar del eje, y como resultado su velocidad de rotación va a disminuir, atrasando respecto de la superficie de la Tierra, y aterrizando en un lugar más al Oeste del inicial.
Un observador situado sobre la superficie, evidentemente, debe observar el mismo desplazamiento del proyectil respecto al suelo. Pero como no puede percibir la rotación de la Tierra no puede hacer el mismo análisis que nosotros. Este observador nota el mismo cambio en la velocidad del proyectil relativa al suelo, y por las leyes de Newton deduce que una fuerza debe estar actuando sobre éste, aunque su origen es desconocido. Ésta es la fuerza de Coriolis.
MOVIMIENTO EN DIRECCIÓN ESTE-OESTE
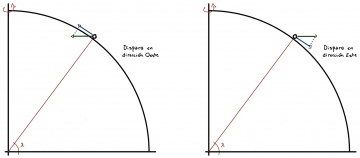
Supongamos nuevamente que nuestro cañón está en algún punto con latitud λ. El cañón no está adherido a la superficie, sino que simplemente está apoyado, y se mantiene en reposo respecto al suelo gracias a la acción de la gravedad terrestre. Por estar describiendo una trayectoria circular el cañón acelera hacia el eje de rotación, pues de otra forma se desplazaría sobre la superficie. La fuerza que le imprime esa aceleración no es otra que la gravedad; podemos pensar que parte del peso del cañón (y el proyectil en su interior) se invierte en modificar constantemente su velocidad para mantenerlo en reposo sobre la superficie, de manera que lo que medimos con una balanza no es el total de la acción de la gravedad, sino la fuerza neta que queda tras confinarlo a estar en el suelo. Pero disparemos ahora el proyectil. Si lo disparamos hacia el Este la velocidad v que le imprime el cañón se va sumar a la velocidad de rotación de la Tierra, y como ahora la velocidad neta es mayor hace falta invertir una parte mayor del peso para confinarlo sobre la superficie. En dirección vertical la tendencia a alejarse va a ser compensada por el peso (el que medimos con la balanza), pero en la dirección horizontal no hay fuerza para compensar. La siguiente figura ilustra esta situación.
El resultado entonces es que el proyectil va a alejarse en dirección Sur si estamos en el hemisferio norte, y en dirección Norte si estamos en el hemisferio sur. La trayectoria, por lo tanto, se desvía hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur. Si, por el contrario, disparamos hacia el oeste, la velocidad v se va a restar de la velocidad de rotación de la Tierra; la velocidad neta va a ser menor y por lo tanto una parte menor del peso es necesaria para confinar el proyectil a la superficie. Como ahora la gravedad hace más fuerza de la necesaria en dirección hacia el eje de rotación y no hay otra fuerza que la compense en dirección paralela al piso, el resultado es que el proyectil va a acelerar hacia el Norte (hacia la derecha) en el hemisferio norte y hacia el Sur (hacia la izquierda) en el hemisferio sur.
Un observador sobre la superficie de la Tierra va a ver el mismo desplazamiento del proyectil respecto al suelo, pero al no percibir la rotación de la Tierra se ve obligado a concluir que una fuerza de origen desconocido acelera el proyectil apartándolo de una trayectoria que, de otra manera, sería recta. Esta es la aceleración de Coriolis.
Vemos entonces que tanto en la dirección Norte-Sur como en la dirección Este-Oeste la rotación de la Tierra deflecta las trayectorias hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur. No solamente eso, sino que es posible demostrar que en los dos casos la aceleración hacia la derecha de la trayectoria es de la misma magnitud: 2ωvSen(λ), donde ω es la velocidad angular de la Tierra, y v y λ son la velocidad del proyectil respecto a tierra y la latitud, como siempre. Podemos describir entonces al efecto Coriolis como una tendencia de los cuerpos en movimiento a retornar a su posición inicial, que es despreciable cerca del ecuador, y se hace más importante a medida que nos acercamos a los polos. La baja velocidad angular ω de la Tierra (una revolución cada 24 hs) hace que el efecto no sea apreciable a la escala en la que hacemos la mayoría de las cosas. Así, mientras elefecto Coriolis es importante para el disparo de un misil intercontinental, que tiene un gran tiempo de vuelo, es completamente despreciable para alguien practicando tiro en un polígono.
La aceleración de Coriolis tiene gran importancia para la meteorología, pues es un efecto con una fuerte incidencia en el movimiento de grandes masas de aire. La siguiente imagen, tomada por el satélite METEOSAT-7 (https://es.wikipedia.org/wiki/Meteosat) EN 2011, representa una espectacular manifestación del efecto Coriolis
En la imagen, prácticamente sobre el mismo meridiano se muestran dos ciclones ocurriendo simultáneamente: Thane, Al norte del Ecuador y sobre la costa India, y Benilde, al sur del Ecuador y sobre el océano Índico. Debido a que están en diferentes hemisferios estos ciclones rotan en sentido contrario. El ciclón Benilde rota en sentido horario mientras Thane rota en sentido antihorario.
Debug data: